来源:上海科技馆
作者:郭玮宏
每次在做核酸的时候,看着前面长长的队伍,我都在想,什么时候才能排到我呢?为什么我排的队总是比别人慢呢?到底什么时候下楼排队,才是最好的呢?

其实,核酸排队也是一门学问。如果排队的人太多而核酸检测点太少,则大家排队会等太久,如果为了大家不排队而增加大量核酸检测点,则浪费了医疗资源。
那么怎样减少排队时间、优化服务资源投入?数学家早就研究过了,并由此发展出了运筹学的一个分支——排队论。
排队论起源于1909年,丹麦数学家、电气工程师埃尔朗最早用概率论方法研究哥本哈根市电话局的电话占线问题,那时急需解决一个重要难题:电话公司应该设置多少台交换机、雇佣多少接线员?埃尔朗用数学语言描述了随机打电话的人和随机通话的时间,能够解答任意数量接线员和接线机问题。他在1909年发表“概率论与电话会话”论文被公认为排队论的开山之作。
除了做核酸,我们日常生活中经常遇到的现象,如到商店购买东西、到医院看病、十字路口堵车,都是排队问题。类似于电话占线、机器故障维修、乃至于牛奶供应配送等,都是无形的排队。
那么数学家对排队问题研究出了什么呢?
基本概念
首先是排队论的基本模型。
非常简单,就是顾客到达服务台接受服务,有人的话就排队,排到就接受服务,接受好服务就离开。这是排队论最基本的模型描述。核酸排队的基本模型,就是居民来到核酸检测点排队,排到就进行核酸检测,做完就离开。

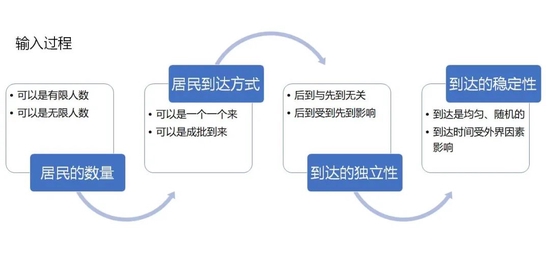
一般的排队过程都由输入过程、排队规则、服务过程三部分组成、
输入过程是指顾客到来时间的规律性。对于核酸检测来说,可以看作居民是无限的,独立、均匀、随机地到来。此处所谓“无限”,是指核酸检测容量是无限的,即道理上可以无限排队下去,而不是指人数本身是无限的。与之相对“有限”的概念,可以看做停车场车位是有限的,排队来停车,能排到就停,排不到就要开走。“无限”和“有限”是两种不同的模式。
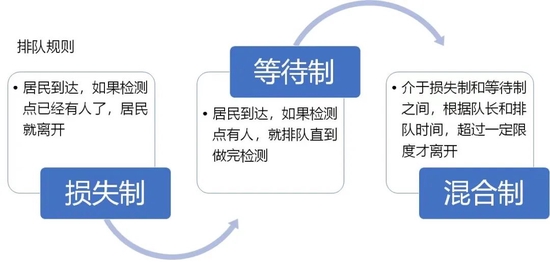
排队规则指到达排队系统的顾客按怎样的规则排队等待。可分为损失制,等待制和混合制三种。核酸检测显然是等待制。
服务过程主要包括服务机构和服务规则两部分。
服务机构放在核酸检测这件事来说,就是可以有1组或多组大白在同时检测,多组检测又存在并联或者串联的形式。相信对于不同小区来说,会是不同的服务模式。



等待制的服务规则有先到先服务、先到后服务、优先服务和随机服务几种模式。通常排队论研究的都是先到先服务模式,核酸检测也明显是先到先服务模式。
最后,我们要假设服务是随机且均匀平稳的。这样的分析才有意义,比如大白在中午去吃饭了,这时候研究怎么排队是没什么意思的。
哪些因素会影响排队模型的分类?
D.G.Kendall(1953)提出对排队模型分类方法影响最大的特征有三个:
X:相继顾客到达间隔的时间分布
Y:服务时间的分布
Z:服务台的个数
根据这3个特征,排队模型的Kendall记号为:X/Y/Z。后来在1971年国际排队符号标准会上将Kendall分类记号扩充到六项,记为X/Y/Z/A/B/C,表示:输入分布/输出分布/并联的服务台数/系统容量(队长)/系统状态(顾客有限或无限)/服务规则。
核酸排队问题的求解
求解排队问题的目的,是研究排队系统运行的效率、估计服务质量、确定系统参数的最优值,以决定系统结构是否合理、研究设计改进措施等。因此必须确定用以判断系统运行优劣的基本数量指标,也称为系统运行指标。
核酸排队中,我们主要关注这些指标:


泊松分布
如何能够准确描述核酸检测的排队状态呢?常用的描述排队状态的分布有泊松分布、确定型分布,指数分布和爱尔朗分布等。核酸检测居民到来的分布和检测点能够服务人员的分布都可以视为泊松分布。
泊松分布
生活中最常见的随机均匀的发生概率的描述就是泊松分布,由法国数学家西莫恩·德尼·泊松在1838年时发表,用来描述单位时间内随机事件发生的次数的概率分布。
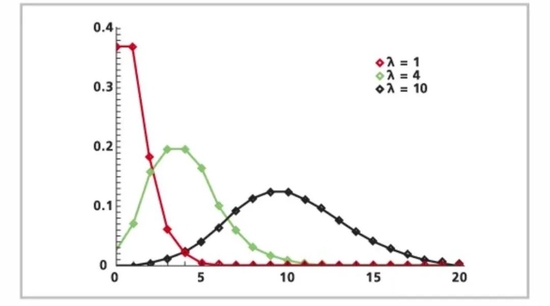
图源:blog.csdn.net
泊松分布的状态概率函数如下:
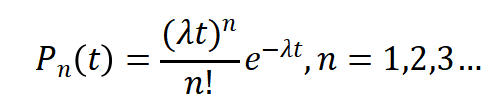
前面介绍已经说过,核酸检测居民到来的分布和检测点能够服务人员的分布都可以视为泊松分布,那么在公式中这个参数λ可以表示单位时间平均到达的居民数,用μ表示单位时间完成核酸检测的居民数,则1/λ表示居民到达的平均时间间隔,1/μ表示一个居民的平均核酸检测时间。
算一算
考虑到我们小区是前面说过的多队列多检测点模式,对于1队来说就是单队列单检测点,我们把这个排队模式记为M/M/1(还记得那个X/Y/Z吗?):M就是指负指数分布(泊松分布是一种负指数分布),第一个M是指居民相继到达时间服从参数为的负指数分布,第二个M是指服务时间服从参数为的负指数分布,服务台个数为1,且允许无限排队,这是一类最简单的排队系统。
于是有:
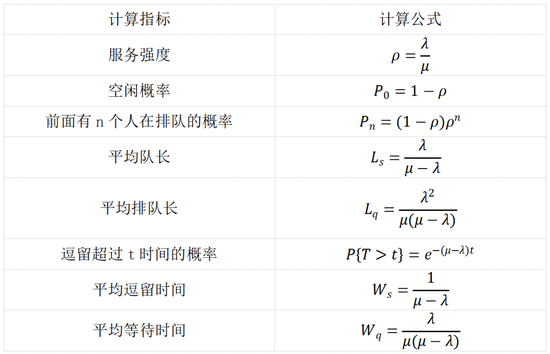
在上述公式中,服务强度体现了系统的繁忙程度。只有ρ<1,系统才有平衡状态。大家可以想想,如果ρ>1会发生什么。
好了,铺垫了这么多,终于可以进行一些计算了。
假设:我们小区有3000人,5小时测完,总共3个检测点,那么1个检测点1分钟平均到达约3.33个人。且假设15秒能检测完1个人(差不多吧),也就是1分钟检测4个人。
根据假设:λ=10/3,μ=4,ρ=λ/μ=5/6
代入公式得出

这样计算的结果似乎与大家的实际体验比较不符,这是因为实际中居民往往是在同一时间出现,不满足均匀分布的假设,且大白在给小朋友检测时,也做不到15s测完1个人。这就导致某些时候,到达的人远远多于能够离开的人,也就是服务强度ρ>1,这个时候就会出现拥堵,持续下去人会越聚越多,只能让后面的人先不要来慢慢消化了。
不过本文的计算也提示我们,其实只要安排好居民出现的时间尽量均匀,排队并不需要很长。
总而言之,战胜疫情还需要我们一同努力,该排队的时候大家也会认真排队,不管队伍多长。那么本文就留给大家排队的时候慢慢看吧。

[1][运筹学]课程精讲 | 9.1 排队论的基本概念。 https://www.bilibili.com/video/BV14A41147zh?spm_id_from=333.337.search-card.all.click
[2]排队论模型(一):基本概念、输入过程与服务时间的常用概率分布。https://blog.csdn.net/qq_29831163/article/details/89735320
[3]如何用简单易懂的实例解释排队论?https://www.zhihu.com/question/316750026
电话新冠肺炎上一篇 没有了